Les mathématiques des carrés magiques

Que ce soit dans Minnie Mag ou dans votre bouquin de maths de 6ème, vous êtes forcément tombé un jour sur un carré magique comme celui montré ci-contre. En général, le carré n'est pas complété et le jeu consiste à caser les nombres manquants en satisfaisant les conditions suivantes : la somme des nombres d'une colonne, d'une ligne ou d'une diagonale doit toujours donner le même résultat (15 dans notre exemple). Quelles propriétés mathématiques se cachent derrière ces amusantes constructions ? Quelles méthodes utilise t-on pour les concevoir ?

J'ai adapté ce billet en vidéo animée, mais l'article est encore là, juste en dessous :)

Ces curiosités mathématiques sont connues depuis des lustres, on sait que les chinois jouaient déjà avec en -650. Les Indiens, puis les arabes s'en amusèrent, les mêlant à toutes sortes de jeux cabalistiques ou religieux. Les arabes seraient les premiers à les avoir considérés comme des objets mathématiques et à étudier leurs propriétés. Un diplomate français (également poète et anthropologue avant l'heure), Simon de la Loubère, rapporta du Siam le terme "carré magique". Bien plus tard, le célébrissime Pierre de Fermat étudiera les cubes magiques.

Comment construire un carré magique ?

De nombreuses méthodes existent pour construire des carrés magiques, je vous présente la mienne, que je tiens de mon instituteur de CM2, Serge Frère. Je pars de l’exemple donné précédemment: un carré d'ordre 3 (avec 3 colonnes et 3 lignes) où il faut disposer les nombres 1, 2, 3, 4, 5, 6, 7, 8 et 9. Remarquez que ces nombres se suivent, ils forment ce qu'on appelle une suite mathématique. Je reviendrai là dessus plus tard, pour l'instant, voyons comment il faut les arranger de façon à ce que le carré soit "magique".

Le carré ainsi formé (que j'appelle B) est bien un carré magique, mais je remarque qu'il n'est pas le même que celui de l'exemple (que j'appelle A). C'est parce qu'il existe plusieurs carrés magiques d'ordre 3. Des opérations de symétrie permettent de passer d'une version à l'autre. Ainsi, pour retomber sur A, on doit d'abord prendre l'image de B dans un miroir (on obtient B'), puis effectuer une rotation d'un quart de cercle dans le sens des aiguilles d'une montre (on obtient B" qui est exactement le même carré que A):

Comme il existe 4 rotations ayant chacune une image miroir, cela fait 8 versions possibles pour un carré magique d'ordre 3. Mine de rien, vous venez d'utiliser des matrices et des opérations de symétrie. Si vous n'aimez pas les maths, c'est un grand pas en avant !

Les carrés magiques et les suites arithmétiques

Un carré magique arabe peint sur un bol chinois

Cette méthode de construction peut être utilisée pour construire d'autres carrés magiques: il suffit pour cela d'avoir une suite mathématique, c'est à dire une suite logique de nombres où une règle simple permet de passer d'un nombre au suivant. Pour remplir les cases du premier exemple (le carré A), on utilise les nombres 1, 2, 3, 4, 5, 6, 7, 8 et 9. Dans cette suite mathématique, pour passer d'un nombre à l'autre, on ajoute 1. Ce nombre qu'on ajoute est appelé raison et il est noté r. Toutes les suites où l'on peut calculer un nombre à partir du précédent en ajoutant une raison r sont appelées suites arithmétiques. Je vais limiter le vocabulaire mathématique à partir de maintenant, c'est promis !

Il existe une infinité de suites arithmétiques, on peut par exemple considérer la suite suivante: 2    4    6    8    10    12  … Ici, chaque nombre se déduit du précédent en ajoutant « 2 ». On a donc r = 2.
On peut prendre n'importe quelles valeurs pour r et pour le point de départ de la suite, par exemple r = 103 et 8 comme point de départ. On a alors une suite arithmétique qui commence comme ça : 

8, 111, 214, 317, 420, 523, 626, 729, 832, 935, 1038   ...

Pour construire un carré magique d'ordre 3, on peut utiliser n'importe quelle suite arithmétique, il suffit d'y choisir 9 nombres consécutifs. Voici un exemple construit avec la suite précédente :

Il est intéressant de noter que le nombre du milieu est toujours égal à la moyenne des 9 nombres du carré. Quant à la somme calculée sur les lignes, les colonnes et les diagonales, elle égale au tiers de la somme de tous les nombres (parce qu'on a un carré d'ordre 3).

Les carrés magiques et les suites géométriques

Sur le modèle précédent, il est possible de construire des carrés magiques en utilisant des suites où les termes successifs sont obtenus en multipliant le précédent, toujours par le même nombre. Ces suites sont dites géométriques. Voici une suite géométrique très simple :

2    4    8    16    32    64    128    256    512    1024    2048    ...

Chaque terme est obtenu en multipliant le précédent par une constante, également appelée raison et notée q pour ne pas la confondre avec la raison des suites arithmétiques (ici q = 2). Comme pour les suites arithmétiques, il existe une infinité de suites géométriques pour lesquelles on peut choisir n'importe quel point de départ et n'importe quelle raison. Pour construire un carré magique à partir d'une suite géométrique, on procède comme auparavant. Mais cette fois, c'est le produit (la multiplication) des nombres qui sera constante dans les colonnes, les lignes et les diagonales. Voici ce que ça donne avec la suite géométrique donnée en exemple (je prends aussi 9 nombres consécutifs) :

Pour chaque colonne, ligne et diagonale, le produit des nombres est égal à 2 097 152, c'est à dire 2 à la puissance 21 (ou 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 pour ceux qui n'aiment pas les puissances). Pour savoir à quoi correspond ce nombre, on peut récrire le carré magique en utilisant des puissances de 2 :

Cette fois, c'est la puissance du nombre au milieu du carré qui est égal à la moyenne des puissances (63/9=7).  Le nombre 21 est lui égal au tiers de la somme de tous les nombres du carré. Autrement dit, en additionnant les puissances le long d'une colonne, d'une ligne ou d'une diagonale, on trouve 21. Cette propriété est intéressante car cela veut dire qu'on peut passer d'un carré magique additif à un carré magique multiplicatif très facilement: il suffit d'élever un nombre constant (2 dans notre exemple) à la puissance indiquée dans la case du carré magique additif pour obtenir un carré magique multiplicatif.

Il existe une méthode toute simple pour former ce carré, elle est donnée ci-dessous et permet de générer le plus petit carré magique multiplicatif d'ordre 3 avec a = 2 et b = 5 (crédits: C.BOYER).

P=a³b³

ab²	1	a²b
a²	ab	b²
b	a²b²	a

Il est même possible de construire des carrés magiques additifs ET multiplicatifs, comme dans le carré magique ci-dessous,  qui possède une constante additive de 840 et une constante multiplicative de 2 058 068 231 856 000 (pioché sur Wikipédia.)

46	81	117	102	15	76	200	203
19	60	232	175	54	69	153	78
216	161	17	52	171	90	58	75
135	114	50	87	184	189	13	68
150	261	45	38	91	136	92	27
119	104	108	23	174	225	57	30
116	25	133	120	51	26	162	207
39	34	138	243	100	29	105	152

Des carrés magiques plus grands

Une plaque du 14 ème siècle gravée d'un carré magique d'ordre 6.

Vous pouvez construire, toujours avec la même méthode, des carrés magiques beaucoup plus grands! Le problème avec ma technique, c'est qu'elle ne fournit que des carrés magiques d'ordre impair. Voici par exemple les étapes de construction d'un carré magique d'ordre 7, c'est un tout petit plus compliqué, mais c'est le même principe. Pour faire très simple, j'ai utilisé la suite arithmétique suivante (avec un point de départ à 1 et une raison r = 1) :

1   2   3   4   5   6   7   8   ...   ....    47   48   49

On commence par rajouter des cases à l'extérieur du carré, puis on les remplit dans l'ordre, comme dans le premier exemple :

Pour remplir le carré, on permute les éléments par "blocs". On peut commencer par les blocs de deux nombres :

On permute ensuite les nombres restants, en les plaçant à l'opposé, comme tout à l'heure (je ne dessine pas toutes les flèches pour ne pas surcharger) :

Et voilà le travail ! Un beau carré d'ordre 7 amoureusement travaillé sous Paint ! Cette fois, le nombre central est 25 : c'est encore la moyenne des 49 nombres du carré. A quoi correspond la somme égale à 175 ? C'est le septième (1 divisé par 7) de la somme des 49 nombres du carré. Pour s'en convaincre, on peut calculer cette somme grâce à cette petite formule (voir la fin d'article pour la petite histoire) :

Somme = (1/2) x (1er nombre + dernier nombre) x (nombre de nombres)

Dans note cas, cela donne: 1/2  x (1 + 49) x (49) = 1225. Si l'on divise cette somme par 7, on retrouve 175. Question: combien de configurations y a t-il pour un carré magique d'ordre 7 ?

Les carrés d'ordre pair

Un carré magique d'ordre 4

Les méthodes de construction des carrés magiques d’ordre pair sont un peu plus complexes, je ne les détaillerai donc pas ici. De plus, comme il n'y a pas de case centrale autour de laquelle on peut faire tourner les autres, il est difficile de parvenir à trouver toutes les configurations pour un ordre donné. Vous trouverez plusieurs méthodes de construction sur internet, comme celles développées sur cette page. Sur l'illustration ci-contre, on peut voir un carré magique d'ordre 4 gravé sur une pierre du temple Parshvanath Jain à Khajuraho, en Inde. Voici sa transcription (crédits: Wikipédia) :

7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

Les propriétés d'addition des carrés magiques

Dans cette formidable vidéo de MicMaths, Mickaël Launay évoque quelques astuces utilisées par un candidat au jeu télévisé de TF1 "Les Extraordinaires". Le candidat semble être un génie des maths, mais en décortiquant sa méthode, on se rend compte qu'il a simplement mémorisé un carré magique, et qu'il a appliqué quelques règles élémentaires pour en construire un nouveau. Bon, le mec compte vite quand même !

Les cubes et les hypercubes magiques

Pour ne pas s'arrêter en si bon chemin, des mathématiciens comme Pierre de Fermat étudièrent l'équivalent tridimensionnel des carrés magiques: les cubes magiques. Le principe reste le même, mais cette fois, les nombres arrangés dans le cube doivent satisfaire à des conditions supplémentaires : la somme des nombres de chaque ligne et colonne selon les 3 axes et les quatre diagonales spatiales principales doit être égale à un même nombre unique. Avec les nombres 1, 2, 3, 4 .. ... n, la constante magique (voir appendice à la fin de l'article) du cube est alors égale à :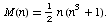

  

Il a été démontré qu'il n'existe pas de cube magique d'ordre 2, 3 et 4. Le premier cube parfait (ordre 7) a été trouvé par le Révérend A. H. Frost en 1866. Par la suite, des cubes magiques d'ordre 8, 9, 10, 11 et 12 furent construits (lire ici pour plus de détails). Le plus petit cube magique fut découvert il y a dix ans tout juste, le 13 Novembre 2003 exactement. Le développeur informatique français Christian Boyer et le professeur de maths allemand Walter Trump exhibèrent un hypercube magique d'ordre 5 (et prouvèrent son existence par la même occasion).

Cube magique d'ordre 5. Crédits : Bruno Bourgeois, B2 Infographie. Copyright "Sciences et Avenir"

De la même façon, les mathématiciens ont imaginé des hypercubes de dimension supérieure à 3. Cette fois, on ne peut plus se représenter ce que cela donne mais les mathématiques ne s’embarrassent pas de tels détails. Il suffit d'exprimer les éléments de ces hypercubes sous forme de matrices. Celles ci génèrent des espaces vectoriels de dimension n qui respectent encore les mêmes conditions d'addition le long des n lignes et selon les n axes.

Représentation graphique d'un hypercube en 9 dimensions

Pour en savoir plus et jouer : la page de Thérèse Eveilleau.
Pour avoir une vue d'ensemble : la page wiki
Pour (presque) faire le tour de la question : ce site
Pour devenir un pro et gagner du fric: cette page
Pour en apprendre plus sur les cubes magiques : cette page

Appendice : Calcul de la somme des termes d'une suite géométriques

Comme la pomme de Newton ou le bain d'Archimède, la formule qui permet de calculer la somme des termes (les nombres successifs qui composent une suite) a sa petite légende. C'est Carl Friedrich Gauss, le Mozart des Maths, qui a trouvé cette méthode de calcul. Une petite anecdote, citée dans l'éloge funèbre de Wolfgang Sartorius (un géologue allemand), est à l'origine de ce qui est vraisemblablement un mythe :

« Le jeune Gauss venait juste d'arriver dans cette classe quand Büttner donna en exercice la sommation d'une suite arithmétique. À peine avait-il donné l'énoncé que le jeune Gauss jeta son ardoise sur la table en disant « la voici ». Tandis que les autres élèves continuaient à compter, multiplier et ajouter, Büttner, avec une dignité affectée, allait et venait, jetant de temps en temps un regard ironique et plein de pitié vers le plus jeune de ses élèves. Le garçon restait sagement assis, son travail terminé, aussi pleinement conscient qu'il devait toujours l'être une fois une tâche accomplie, que le problème avait été correctement résolu et qu'il ne pouvait y avoir d'autre réponse. »

Comment le petit Carl Friedrich s'y était il pris pour faire en 30 secondes ce qui occuperait une classe une bonne demi-heure ? La petit génie avait trouvé une belle astuce: en écrivant la somme deux fois, une première fois dans l'ordre, une seconde fois à l'envers, il avait remarqué que les termes formaient des paires dont la somme était constante.

Ainsi disposés, il est facile de calculer la somme des termes: toutes les paires ont une somme égale à 101. Combien y a t-il de paires? Il y en a 100 (on a écrit tous les nombres entiers de 1 à 100). On a donc:

2 Sommes = 100 x 101, ou encore Somme = (100 x 101)/2

Plus généralement, on démontre en utilisant la même méthode, que la somme des termes consécutifs d'une suite arithmétique (additive) est obtenue en additionnant le premier et le dernier terme, en multipliant ce résultat par le nombre de termes et en le divisant par 2.

En utilisant les notations mathématiques, on obtient cette formule où p et n sont des entiers, p étant inférieur à n et où Un désigne le n^ème terme de la suite: