Commençons par la première partie de l'expérience, on verra après pour les explications :
Il suffit de disposer le chocolat ou le fromage (ou les deux mais ce sera immangeable après) sur une assiette et d'enfourner le tout pendant 20 secondes en ayant pris soin de retirer le plateau tournant, sinon l'expérience foire lamentablement! En sortant l'assiette, vous devriez vous retrouver avec un truc comme ça : |
| Un mars après passage dans un micro-ondes, crédits : Philosophy of Science Portal |
Votre chocolat devrait être fondu à certains endroits précis, comme sur la photo (si ce n'est pas le cas, changez l'assiette de direction et repassez-la au micro-onde). Pour comprendre pourquoi, il faut tout d'abord se rappeler comment le four à micro-ondes fonctionne. Si vous êtes pressés de manger, mesurez l'écart entre deux zones fondues consécutives au préalable. Ne vous brûlez pas et lisez la suite.
Le four à micro-ondes
 |
| Représentation d'une molécule d'eau |
Les ondes stationnaires
Comment se fait-il que le chocolat soit liquide en certaines zones et pas d'autres ? Pour répondre à cette question, il va falloir parler un tout petit peu des ondes. Une onde est la propagation d'une perturbation qui affecte sur son passage les propriétés physiques du milieu. Cela peut être une variation de pression (onde acoustique), de hauteur (vague dans la mer) ou même un ralentissement sur l'autoroute. Les ondes émises dans le four sont des ondes électromagnétiques, c'est à dire qu'elles affectent les champs électriques et magnétiques (qui sont indissociables). Elles ont cette forme :
 |
| Représentation d'une onde électromagnétique |
 |
| Visualisation de la propagation d'une perturbation electromagnétique. Crédits : Jacob Dilles, ici |
Elles provoquent des variations continues du champ en tout point du four avec une fréquence de 2,45 GHz, c'est à dire 2 450 000 000 Hz. Cela signifie que, si en un point, à un instant, le champ est maximal et orienté vers le haut, alors il sera de nouveau maximal et orienté vers le haut 0,4 milliardièmes de secondes plus tard (1 divisé par 2 450 000 000). Sur l’illustration, on voit également la longueur d'onde (notée lambda) qui correspond à
la distance entre deux états identiques de l'onde (2 maximums par
exemple).
Comme ces ondes sont émises dans une enceinte fermée, elles sont réfléchies par les parois et se superposent, créant des ondes dites "stationnaires". Au lieu de varier continuellement au cours du temps, le champ prend des valeurs nulles et maximales en certains points fixes. Cette petite animation permet de visualiser le phénomène, on peut y voir deux ondes se propageant en sens contraire. L'onde résultante (la superposition des ondes rouge et bleue, est une onde stationnaire.
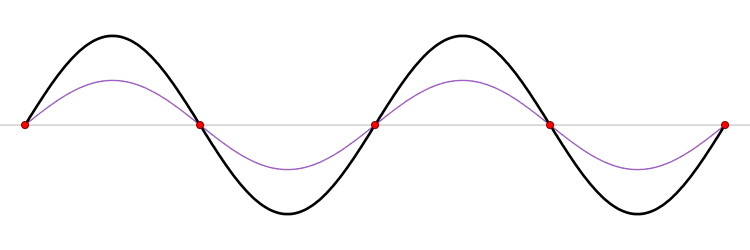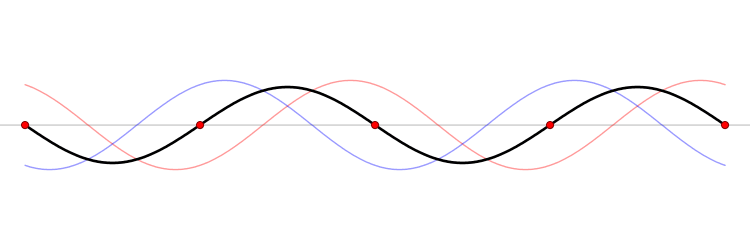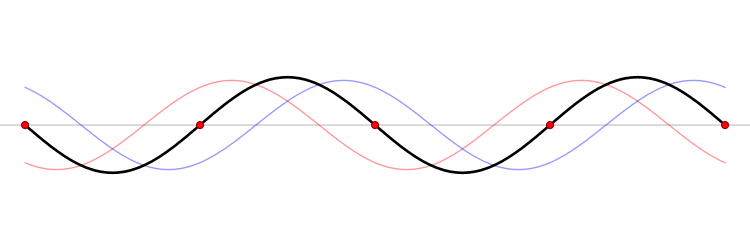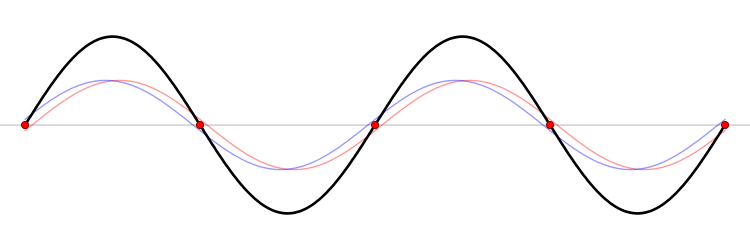 |
| Onde stationnaire, crédits : Wikipédia |
Les points où le champ est nul sont appelés "nœuds" et les points où le champ est maximal, "ventres". A proximité des nœuds, le champ est très faible voire nul. Les molécules d'eau ne sont donc pas très agitées et la température peu élevée. A l'opposé, aux points où le champ est très fort, les molécules d'eau sont très excitées et dégagent beaucoup de chaleur. Ceci a pour effet de créer des zones plus ou moins fondues dans votre chocolat. Pour remédier à ce problème, les fabricants équipent leurs fours d'un plateau tournant et de dispositifs de diffraction (les petits trous et les renfoncements à l'intérieur).
Dans la suite de cette expérience, on ne considère que les ondes qui se propagent dans l'axe de la longueur du four. En réalité, les ondes se propagent dans toutes les directions, se superposent et créent un motif beaucoup plus complexe. L'image ci-dessous, tiré de l'article "Peut-on vraiment mesurer la vitesse de la lumière avec un four microonde et du chocolat ?" montre comment se répartissent vraiment les ventres et les nœuds :
Dans la suite de cette expérience, on ne considère que les ondes qui se propagent dans l'axe de la longueur du four. En réalité, les ondes se propagent dans toutes les directions, se superposent et créent un motif beaucoup plus complexe. L'image ci-dessous, tiré de l'article "Peut-on vraiment mesurer la vitesse de la lumière avec un four microonde et du chocolat ?" montre comment se répartissent vraiment les ventres et les nœuds :
 |
| Visualisation de la structure réelle de l'onde stationnaire dans un four à l'aide d'une caméra de thermographie infrarouge. Vollmer M, Physics of the microwave oven, Physics Education, 2004, 39:74-81 |
Calcul de la vitesse de la lumière
 |
| L'onde stationnaire dans le micro-onde, crédits : ici |
λ = c / f
où c est la vitesse de la lumière, λ (Lambda) la longueur d'onde et f, la fréquence. La vitesse de la lumière est donc égale à λ multiplié par f :
0,12 x 2 450 000 000 = 294 000 000 m.s-1
ce qui est une assez bonne estimation de la vitesse de la lumière (299 792 458 m.s-1), compte tenu de l'imprécision du dispositif.
Pour ma part, j'avais mesuré une longueur d'onde similaire avec une assiette de fromage rappé. Il faut croire que j'ai eu de la chance ou que j'ai inconsciemment judicieusement choisi une zone compatible avec les résultats que j'espérais ! Si vous réalisez l'expérience, n'hésitez pas à me communiquer vos résultats !
Une petite anecdote pour finir : l'idée du four à micro-ondes revient à Percy Spencer, un ingénieur de la firme Raytheon, spécialisée dans les radars. En travaillant à proximité d'un radar (qui fonctionne avec des micro-ondes), il s’aperçoit que la barre chocolatée dans sa poche commence à fondre et que les conditions de sécurité sur son lieu de travail laissent à désirer. Il dépose en 1945 un brevet pour un nouveau type de four : le "radarange". The rest is History.
« 2,45 MHz, c'est à dire 2 450 000 000 Hz »
RépondreSupprimerSorry about that, mais il me semble que 2,45 MHz, c'est 2,45 × 10⁶ Hz, ce qui donne 2 450 000 Hz !
2.45 Ghz et non pas Mhz
SupprimerAbsolument!!! Il faut que je fasse plus attention! Je corrige ça tout de suite..
RépondreSupprimerMais un four à micro-ondes ce n'est pas 2.45 GHz ? :)
RépondreSupprimerSi, j'avais laissé trainer des mégahertz ! J'espère que c'est bon cette fois. Et promis, je ne me recyclerai pas en comptable !
RépondreSupprimerL’expérience est intéressante et sympathique mais d’après Jean-Michel Courty et Edouard Kierlik (qui écrivent les Idées physiques tous les mois dans Pour La Science) ont montré que ce résultat ne tenait fasse à la structure des ondes électromagnétiques dans un micro-onde :
RépondreSupprimerhttp://blog.idphys.fr/2011/mesurer-la-vitesse-de-la-lumiere-dans-un-four-microonde-ce-nest-helas-pas-aussi-simple/
Excellent ! Je vais revoir complètement mon truc.. De mon côté, j'avais réalisé l'expérience avec une assiette de fromage rappé et ça donnait un truc pas trop mal ! Merci :)
RépondreSupprimerJacques Grimault lui parvient à mesurer la vitesse de la pyramide avec un rouleau de PQ et une pyramide... Tout le monde ne peut pas avoir sa classe... ^^
RépondreSupprimerbonjour mes chers caribou je ne comprend pas pourquoi vous me lechez la nuit aidez moi
RépondreSupprimer93 en force
RépondreSupprimer69 represente
RépondreSupprimeralcolique anonyme
RépondreSupprimerje veut une reponse
RépondreSupprimerohoh ila quelqu'un
RépondreSupprimerOui y'a quelqu'un,réponse à l'anonyme du 4 juin 2015 depuis décembre 2016,personne entre temps,ça fait peur ce vide sidéral, une bonne estimation de la vitesse de la lumière.
RépondreSupprimer